Mr Art Mountain, our Mathematician-in-Residence, delivers weekly sessions to our lower school pupils at MathsSci Club on Mondays at 1.45pm in M5.
Please find below a report about the latest sessions from Year 8 pupils Charlotte, James, Ayden and Christopher
Fractals (& Dimensions)
One of the topics we covered was fractals and dimensions. We looked at shapes that are: 0D (a point), 1D (a line), 2D (a flat shape) and 3D (a shape with length, width and depth).
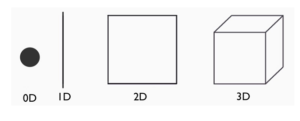
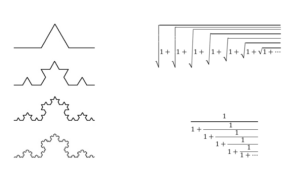
We also discovered that there can also be dimensions in between these ones. Some shapes have dimensions in between two whole dimensions (between 1D and 2D) and we saw that our fractal (on the following photo) was “self-similar” – which means that a small part of the shape looks like the whole shape. Every time you removed a third of the line and joined up the space in between with 2 other lines, then each contained 4 times as many of the original line, meaning it is multiplied by more than one and adds up to dimensional. I found this idea to be incredible because it made me see the world in a whole new dimension!.
Golden Ratio
The Golden Ratio is a number, often denoted by the Greek letter φ (phi) and is approximately equal to 1.618…
It can be defined algebraically as the positive solution to the equation:.
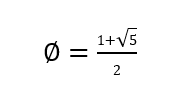
The Golden Ratio a special number, found in several places including nature and artwork. It is an irrational number, meaning it cannot be expressed as the ratio of two integers.
The Golden Ratio has the property that if a line segment is divided into two parts, a and b, then the whole segment a+b is to the longer part a as a is to the shorter part b, then:
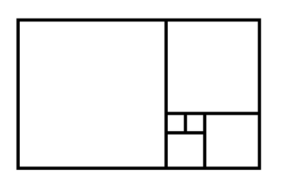
We used a constructible number (any number that can be created with a straight line and a compass).
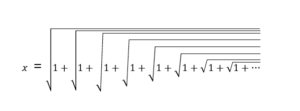
We found that:
![]()
Infinity and Sets
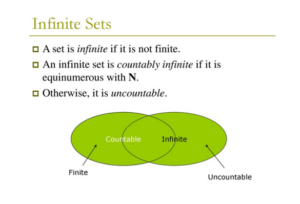
When we were learning about infinity, we studied the mathematical idea of sets, which are groups of things (in this case, numbers). Infinity can be defined as a set whose subsets contain the same number of members as the original group.
For example, the natural numbers (a group of all numbers, shown as ℕ) is a set, and even numbers are a subset of that. The numbers in ℕ can be placed in a one-to-one correspondence with the even numbers (e.g. 1 maps to 2, 2 maps to 4, 3 maps to 6 and so on), meaning there are infinite natural numbers and even numbers.
This also links to countable and uncountable infinity. Countable infinity means that one can count all elements so that even though the counting will take forever, you will get to any particular element in a finite amount of time. However, infinity is a theory and is not an actual number, which is why it cannot be placed in equations such as:
∞ + 2 = …
It is because ∞ is not a number.
Infinity and Paradoxes (Zeno’s)
Another aspect of infinity is the Paradoxes it can create. One example that we learnt about in our session is Zeno’s Paradox. The Paradox is as follows: a hare is chasing after a tortoise, but it will never reach it. This may sound confusing, but the argument is that when it arrives to the point where the tortoise was, the tortoise has moved forward. This repeats itself forever. Obviously, this cannot be true, so here is how we set about proving this using a graph and some equations…
First, we assigned values to the distance, speed, time equation, swapping time for an event, as that is how the Paradox works. Next, we filled out the values, assuming the hare is travelling at 1m/s and the tortoise at 0.5m/s.
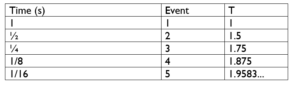
In this case,
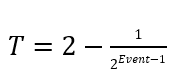
As you can see, at the point recurring graph goes straight upwards, when the hare outruns the tortoise. Because is , which is 1, we can say that is 2. Seeing as the hare is going at 1m/s, and originally 1m away from the tortoise, reaching 2 on the graph proves that the hare will eventually catch up with the tortoise as it is double the speed of the tortoise.













